加密算法用示例解釋
加密是在編碼消息的目的是僅允許預期的收件人理解消息的含義. 這是一個雙向函數(您需要能夠撤消對消息的任何爭奪). 這旨在保護運輸中的數據.
簡單的加密算法
我只是為了娛樂而從事電梯項目,實際上是硬件. 但是我認為這更多是一個軟件問題. 我不需要擁有此功能,實際上它是完全多餘的,但是我很好奇,所以我還是可以添加它,所以我可以學習:P我有一個8位地址,8位數據總線和8位加密代碼. 我有一個主人和許多奴隸設備. 主人知道奴隸的地址,並且知道加密代碼. 奴隸也知道他們的地址和加密代碼. 我想要一種非常簡單的算法,以便:主發送“ y”,y =函數(數據,加密代碼)從屬接收“ y”,並且可以通過data = function2(y,加密代碼)提取數據,我嘗試播放與XOR或等等. 和它們的組合,但無法弄清楚. 再次我正在尋找簡單的算法. 如果您不介意,您可以為我提供更大的恩寵,並解釋我如何獲得這樣的解決方案/功能的理論. 非常感謝!
問2013年4月25日15:46
441 1 1金徽章5 5銀徽章12 12青銅徽章
簡單的 和 有效的加密將以圖書館的形式出現,而不是您自己寫的東西. 僅簡單加密可以是rot13.
2013年4月25日,15:48
XTEA也相對簡單,RC4,但很難正確使用.
2013年4月25日,15:50
一種非常簡單的方法 – 發送y = x xor鍵,然後在另一側x = y xor鍵,但是那裡不會有太多保護.
加密算法用示例解釋
Megan Kaczanowski
密碼學最基本的是使用代碼和密碼保護消息的科學.
加密是在編碼消息的目的是僅允許預期的收件人理解消息的含義. 這是一個雙向函數(您需要能夠撤消對消息的任何爭奪). 這旨在保護運輸中的數據.
如果您正在尋找對稱算法和不對稱算法之間的差異的一般背景以及對加密是什麼的一般概述,請從這裡開始. 本文將主要涵蓋兩種最常用的加密算法.
作為一般概述,首次創建時,對稱算法存在一個主要問題 – 只有雙方已經知道共享的秘密,它們才有效地發揮作用. 如果他們沒有.
如果第三方獲得了鑰匙,那麼他們很容易打破加密,擊敗了安全通信的目的.
Diffie-Hellman通過允許陌生人通過公共渠道交換信息來解決此問題,該渠道可用於形成共享密鑰. 即使所有通信都受到監視,共享密鑰也很難破解.
Difie-Hellman如何工作?
Diffie-Hellman就是所謂的密鑰交換協議. 這是Diffie-Hellman的主要用途,儘管它也可以用於加密(通常不是,因為它更有效地使用D-H來交換鍵,然後切換到(明顯更快)的對稱加密來進行數據傳輸).
此操作的方式如下:
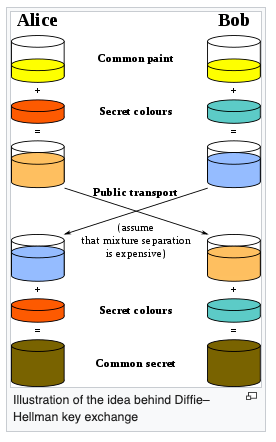
基本上,有兩個政黨,愛麗絲和鮑勃,它們同意起始顏色(任意但每次都必須不同). 他們也有自己保留的秘密色彩. 然後,他們將這種顏色與共享顏色混合在一起,從而產生兩種不同的顏色. 然後,他們將這種顏色傳遞給另一方,後者將其與秘密顏色混合在一起,從而產生了相同的秘密顏色.
這依賴於將兩種顏色混合在一起相對容易的想法,但是很難將它們分開以找到秘密顏色. 實際上,這是通過數學完成的.
- 鮑勃(Bob)和愛麗絲(Alice
- 現在,鮑勃選擇一個秘密號碼x(x = 4),並執行以下操作:x = g^x%p(在這種情況下,%表示其餘部分. 例如3%2是3/2,其中剩餘的為1). x = 5 ^4%29 = 625%29 = 16
- 愛麗絲還選擇了一個秘密號碼,y(y = 8),並執行以下操作:y = g^y%p. y = 5 ^ 8%29 = 390,625%29 = 24
- 鮑勃將X發送給愛麗絲,愛麗絲將Y發送給鮑勃.
- 然後鮑勃做以下內容:k = y ^ x%p,k = 24 ^ 4%29 = 331,776%29 = 16
- 愛麗絲進行以下操作:k = x ^ y%p,k = 16 ^ 8%29 = 4,294,967,296%29 = 16
關於這一點的偉大(*可能是魔術*)的事情是,鮑勃和愛麗絲都有相同的數字,現在可以用它來秘密說話,因為沒有人知道k.
該協議的安全性是基於幾件事:
- (事實)生成質數相對容易,甚至大質數(例如P).
- (事實)模塊化凸起很容易. 換句話說,計算x = g ^ x%p是相對容易的.
- (基於當前計算能力和數學的假設)沒有主要因素的模塊化根提取很難. 本質上,即使您在流量上偷偷摸摸並且可以看到p,g,x和y,也很難找到k不知道x和y。.
因此,假設這是正確實現的,那麼執行創建密鑰所需的數學是相對容易的,但是要嘗試通過蠻力強迫打破鑰匙所需的數學非常困難和耗時.
即使攻擊者能夠妥協此鑰匙,Diffie-Hellman也允許完美的前鋒保密.
什麼是完美的前鋒保密?
這是這樣的想法,如果您破解了服務器現在用來通信的加密,這並不意味著服務器曾經進行的所有通信都可以讀取.
換句話說,它只允許您看到現在正在使用的通信(即使用此秘密鍵). 由於每組通信都有一個不同的秘密鍵,因此您必須單獨破解它們.
如果每個會話都有每個會話的不同短暫鍵,這是可能的. 由於Diffie-Hellman總是為每個會話使用新的隨機值(因此為每個會話生成新密鑰),因此稱為短暫的Diffie Hellman(EDH或DHE). 許多密碼套房都使用此套件來實現完美的前鋒保密.
由於Diffie-Hellman允許您以明文交換關鍵材料,而不必擔心會損害共享的秘密,而且數學對於攻擊者來說太複雜了,無法違反武力,攻擊者無法衍生會話密鑰(即使可以使用,也可以使用每個會話的不同,短暫的鑰匙意味著它們只能在本次會議上窺探 – 在過去或將來都不是).
Effort Secrecy可以通過任何Diffie-Hellman密鑰交換來啟用,但只有短暫的鑰匙交換(每個會話的不同鍵)提供了完美的前鋒保密.
這是斯科特·赫爾姆(Scott Helme)的帖子,更深入地談論這一點,並解釋如何在服務器上啟用此內容.
什麼是Diffie-Hellman的限制?
D-H的最大限制是無法驗證身份. 換句話說,任何人都可以聲稱自己是愛麗絲或鮑勃,並且沒有內置的機制來驗證他們的陳述是真的.
此外,如果不能以安全的方式執行實施,則可以用足夠的專用資源來破解該算法(不太可能,但對於學術團隊或民族國家參與者來說可能).
例如,如果未向隨機數發生器提供足夠的熵以支持所需的強度 – 換句話說,因為計算機生成的數字永遠不是真正的隨機,這可能會發生這種情況。您的實施.
此外,2015年有一次攻擊表明,當許多服務器使用相同的質量數字作為密鑰交換的開始時,Diffie-Hellman的總體安全性低於預期.
本質上,攻擊者可以簡單地預先計算對該素數的攻擊,從而更容易為使用該質數的任何服務器妥協會話.
之所. 預先計算這種類型的攻擊仍然需要學術或民族國家水平的資源,並且不太可能影響絕大多數人.
但是,幸運的是,對於那些不必擔心民族國家攻擊者的人來說,使用橢圓曲線密碼學(ECDHE)實現DH密鑰交換的方法有所不同。. 這是本文的範圍,但是如果您有興趣了解有關此交換背後的數學的更多信息,請查看本文.
有關DH的弱點,請更詳細地查看此白皮書和此網站.
RSA
RSA以創作者的名字命名 – Rivest,Shamir,Adleman – 這是一種產生公共和私人鑰匙的方式.
從技術上講,有兩種RSA算法(一種用於數字簽名,另一種用於非對稱加密.) – 本文涵蓋了不對稱的加密算法.
這允許進行鍵交換 – 您首先將每個方分配給事務公共/私鑰,然後生成對稱密鑰,最後,您使用公共/私鑰對安全地傳達了共享的對稱密鑰.
因為不對稱加密通常比對稱加密慢,並且不尺寸也不太擴展,因此使用不對稱加密來安全交換對稱密鑰非常普遍.
那麼它是怎樣工作的?
- 選擇2個非常大的素數(至少512位或155個小數位數),x和y(這些數字需要是秘密的,並且隨機選擇)
- 找到產品,即Z = X*y
- 選擇一個奇怪的公共整數E,在3和N -1之間,沒有(X -1)(Y -1)的共同因素(1)(因此,它相對較高,因此x -1和y -1 ).
- 找到x -1和y -1的最不常見的倍數,然後稱其為l.
- 根據X,Y和E計算私人指數D,D. de = 1%L. d是e%l的倒數(您知道存在逆,因為e相對質量為z -1和y -1). 該系統之所以起作用,是因為p =(p ^ e) ^ d%z.
- 輸出(z,e)作為公鑰,(z,d)作為私鑰.
現在,如果鮑勃想向愛麗絲發送一條消息,他將使用此公式從純文本(p)中生成Ciphertext(C):
為了解密此消息,愛麗絲計算以下內容:
D和E之間的關係確保加密和解密函數是反轉. 這意味著解密函數能夠成功恢復原始消息,並且在沒有私鑰(z,d)(或主要因素x和y)的情況下很難恢復原始消息.
這也意味著您可以在不損害系統安全的情況下公開Z和E.
您也可以反向使用操作來獲取消息的數字簽名. 首先,您在明文上使用解密操作. 例如,s =簽名(p)= p ^ d%z.
然後,收件人可以通過應用加密功能並將結果與消息進行比較來驗證數字簽名. 例如,m =驗證(s)= s ^ e%z.
通常,完成此操作後,宣傳是消息的哈希,這意味著您只能使用一個指數簽名(無論長度如何).
系統的安全是基於幾件事:
- (事實)生成質數相對容易,甚至大質數(例如x和y).
- (事實)乘法很容易. 找到Z非常容易.
- (基於當前數學的假設)保理很難. 給定z,恢復x和y很難. 它是可以做的,但是需要一段時間,而且很昂貴.
一項估計說,恢復1024位數字的主要因素將需要一年的機器,這是一台耗資1000萬美元的機器. 增加一倍的規模將呈指數級增加所需的工作量(工作數十億倍).
隨著技術的不斷提高,這些成本(以及所需的工作)將減少,但是在這一點上,正確實施的這種加密是不可能妥協的來源.
通常,唯一具有這種金錢和對單一目標的奉獻精神的黑客是民族國家. 另外,如果有一種更簡單的方法來妥協系統(請參見下文),這可能是一個更好的選擇.
4. (事實)模塊化凸起很容易. 換句話說,計算c = p ^ e%z是相對容易的.
5. (事實)模塊化根提取 – 逆轉上述過程 – 如果您具有主要因素(如果您具有z,c,e和主要因素x和y,則很容易找到p,因此c = p ^ e很容易%z).
6. (基於當前的計算能力和數學的假設)沒有主要因素的模塊化根提取非常困難(如果您具有z,c,e,但不是x和y,則很難找到p,使得c = p ^ e% Z,特別是如果A足夠大).
想從更聰明的人那裡了解更多有關數學的信息? 查看本文.
太好了,更好?
這取決於您的用例. 兩種算法之間存在一些差異 – 首先,完美的前鋒保密(PFS),我們早些時候在Diffie -Hellman的背景下談論了這一點. 從技術上講你 可以 生成短暫的RSA鑰匙對,並通過RSA提供完美的前鋒保密性,計算成本要比Diffie-Hellman高得多 – 這意味著Diffie-Hellman是SSL/TLS實現的更好選擇.
雖然兩種算法之間存在一些性能差異(就服務器所需的工作而言),但性能差異通常不足以在選擇另一個時有所不同.
相反,總的來說,確定哪個更好的主要考慮因素取決於您的用例更受支持(例如,在實施SSL時,由於完美的前進性保密,您需要Diffie Hellman)或更受歡迎或更受歡迎的作為行業的標準.
例如,雖然Diffie -Hellman是美國政府批准的,並且在機構機構的支持下,該標準尚未發布- 而RSA(由私人組織標準化)提供了免費的標準,這意味著RSA在私人組織中變得非常受歡迎.
如果您有興趣閱讀更多,那麼這裡有一個很棒的線程.
有興趣學習如何使用加密攻擊? 嘗試這套來自密碼的挑戰.
我對密碼學的了解越多,我認為愛麗絲和鮑勃應該只是親自聊天.
– Paul Reinheimer(@preinheimer)2017年3月13日