Krypteringsalgoritmer forklaret med eksempler

Kryptering koder for meddelelser med det formål at kun give den tilsigtede modtager mulighed for at forstå betydningen af ​​meddelelsen. Det er en tovejsfunktion (du skal være i stand til at fortryde den, du har gjort med beskeden). Dette er designet til at beskytte data under transit.

Enkel krypteringsalgoritme

Jeg arbejder på et elevatorprojekt bare for sjov, det er faktisk hardware. Men jeg tror, ​​dette er mere et software -spørgsmål. Jeg behøver ikke at have denne funktion, faktisk er det helt overflødigt, men jeg var nysgerrig, så jeg tilføjer det alligevel, så jeg kan lære: P Jeg har en 8 bit adresse, 8 bit databus og en 8 bit kryptering kode. Jeg har en master og mange slaveenheder. Mesteren kender slaverne og kender krypteringskoden. Slaverne kender også deres adresse og krypteringskoden. Jeg vil have en virkelig enkel algoritme, således at: masteren sender “y” hvor, y = funktion (data, krypteringskode) Slaven modtager “y” og kan udtrække data efter data = funktion2 (y, krypteringskode) Jeg prøvede at spille rundt med og, xor, eller osv. og kombinationer af dem, men kunne ikke finde ud af det. Igen leder jeg efter enkle algoritmer. Hvis du ikke har noget imod, at du kunne gøre mig en større fordel og forklare en teori om, hvordan jeg kan komme til en sådan løsning/funktioner. Tusind tak!

spurgte 25. april 2013 kl. 15:46
441 1 1 Guld badge 5 5 sølvbadges 12 12 bronze badges

Enkel og Effektiv kryptering kommer i form af et bibliotek, ikke noget, du skriver selv. Bare enkel kryptering kunne være ROT13.

25. april 2013 kl. 15:48
XTEA er også relativt enkel, RC4, men det er lidt svært at bruge korrekt.
25. april 2013 kl. 15:50

En meget enkel tilgang – send y = x xor -nøgle, derefter x = y xor -nøgle på den anden side, men der vil ikke være meget beskyttelse der.

Krypteringsalgoritmer forklaret med eksempler

Megan Kaczanowski

Kryptografi, på sit mest basale, er videnskaben om at bruge koder og cifre til at beskytte beskeder.

Kryptering koder for meddelelser med det formål at kun give den tilsigtede modtager mulighed for at forstå betydningen af ​​meddelelsen. Det er en tovejsfunktion (du skal være i stand til at fortryde den, du har gjort med beskeden). Dette er designet til at beskytte data under transit.

Hvis du leder efter en generel baggrund om forskellen mellem symmetriske og asymmetriske algoritmer og en generel oversigt over, hvad kryptering er, skal du starte her. Denne artikel vil primært dække to af de mest almindeligt anvendte krypteringsalgoritmer.

Som en generel oversigt var der et stort problem med symmetriske algoritmer, da de først blev oprettet – de fungerede kun effektivt, hvis begge parter allerede kendte den delte hemmelighed. Hvis de ikke gjorde det, var det ekstremt vanskeligt vanskeligt at udveksle en nøgle uden en tredjepartsudvikling.

Og hvis en tredjepart opnåede nøglen, var det meget let for dem derefter at bryde krypteringen og besejre formålet med sikker kommunikation.

Diffie-Hellman løste dette problem ved at give fremmede mulighed for at udveksle information over offentlige kanaler, der kan bruges til at danne en delt nøgle. En delt nøgle er vanskelig at knække, selvom al kommunikation overvåges.

Hvordan fungerer Diffie-Hellman?

Diffie-Hellman er det, der kaldes en nøgleudvekslingsprotokol. Dette er den primære anvendelse til Diffie-Hellman, skønt det også kunne bruges til kryptering (det er typisk ikke, fordi det er mere effektivt at bruge D-H til at udveksle nøgler, og derefter skifte til en (markant hurtigere) symmetrisk kryptering til datatransmission ).

Den måde, dette fungerer på, er som følger:

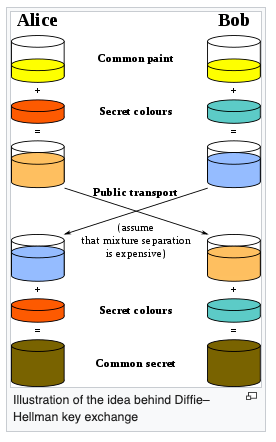
Grundlæggende er der to parter, Alice og Bob, der er enige om en startfarve (vilkårlig, men skal være anderledes hver gang). De har også en hemmelig farve, de holder for sig selv. De blander derefter denne farve med den delte farve, hvilket resulterer i to forskellige farver. De videregiver derefter denne farve til den anden part, der blander den med deres hemmelige farve, hvilket resulterer i den samme ende hemmelige farve.

Dette er afhængig af ideen om, at det er relativt let at blande to farver sammen, men det er meget vanskeligt at adskille dem for at finde den hemmelige farve. I praksis gøres dette med matematik.

1. Bob og Alice er enige om to tal, en stor prime, p = 29, og base g = 5
2. Nu vælger Bob et hemmeligt nummer, x (x = 4) og gør følgende: x = g^x % p (i dette tilfælde % angiver resten. For eksempel er 3%2 3/2, hvor resten er 1). X = 5 ^4 % 29 = 625 % 29 = 16
3. Alice vælger også et hemmeligt tal, y (y = 8) og gør følgende: y = g^y % p. Y = 5 ^ 8 % 29 = 390,625 % 29 = 24
4. Bob sender X til Alice og Alice sender Y til Bob.
5. Derefter gør Bob følgende: K = Y ^ X % P, K = 24 ^ 4 % 29 = 331.776 % 29 = 16
6. Alice gør derefter følgende: k = x ^ y % p, k = 16 ^ 8 % 29 = 4.294.967.296 % 29 = 16

Den store (*muligvis magiske*) ting ved dette er, at både Bob og Alice har det samme nummer, K, og nu kan bruge dette til at tale hemmeligt, fordi ingen andre kender K.

Sikkerheden ved denne protokol er baseret på et par ting:

1. (Faktum) Det er relativt let at generere primtal, endda store primtal (som P).
2. (Fakta) Modulær eksponentiering er let. Med andre ord er det relativt let at beregne x = g ^ x % p.
3. (Antagelse baseret på den aktuelle computerkraft og matematik) Modulær rodekstraktion uden de vigtigste faktorer er meget hård. I det væsentlige er det meget svært at finde K uden at vide X og Y, selvom du har snooped på trafikken og kan se P, G, X og Y.

Forudsat at dette blev implementeret korrekt, er det relativt let at lave den matematik, der kræves for at skabe nøglen, men er ekstremt vanskelig og tidskrævende at gøre den matematik, der kræves for at forsøge at bryde nøglen ved at tvinge den.

Selv hvis en angriber kunne gå på kompromis med denne nøgle, giver Diffie-Hellman mulighed for perfekt fremadrettet hemmeligholdelse.

Hvad er perfekt fremadrettet hemmeligholdelse?

Dette er ideen om, at hvis du knækker krypteringen, som serveren bruger til at kommunikere nu, betyder det ikke, at al kommunikation, som serveren nogensinde har udført.

Med andre ord giver det kun dig mulighed for at se den kommunikation, der bruges nu (dvs. med denne hemmelige nøgle). Da hvert sæt kommunikation har en anden hemmelig nøgle, bliver du nødt til at knække dem alle separat.

Dette er muligt, hvis hver session har en anden, flygtig nøgle til hver session. Fordi Diffie-Hellman altid bruger nye tilfældige værdier for hver session (derfor generering af nye nøgler til hver session) kaldes det ephemeral Diffie Hellman (EDH eller DHE). Mange chiffer suiter bruger dette til at opnå perfekt fremadrettet hemmeligholdelse.

Da Diffie-Hellman giver dig mulighed for at udveksle nøglemateriale i PLAINTEXT uden at bekymre dig om at gå på kompromis med den delte hemmelighed, og matematik Forskellige, flygtige, nøgler til hver session betyder, at de kun kunne snuppe på denne session – ikke nogen i fortiden eller fremtiden).

Fremad hemmeligholdelse er aktiveret med enhver Diffie-Hellman-nøgleudveksling, men kun flygtig nøgleudveksling (en anden nøgle for hver session) giver perfekt fremadrettet hemmeligholdelse.

Her er et indlæg fra Scott Helme, der taler om dette mere dybtgående og forklarer, hvordan du aktiverer dette på dine servere.

Hvad er Diffie-Hellmans begrænsninger?

Den største begrænsning af D-H er, at det er ikke at verificere identitet. Med andre ord kan enhver hævde at være Alice eller Bob, og der er ingen indbygget mekanisme til at verificere, at deres erklæring er sand.

Hvis implementeringen ikke udføres på en sikker måde, kunne algoritmen desuden blive revnet med nok dedikerede ressourcer (usandsynligt, men muligt for akademiske hold eller nationalstatslige aktører).

For eksempel kan dette forekomme, hvis den tilfældige talenerator ikke er forsynet med tilstrækkelig entropi til støtte af din implementering.

Derudover blev der demonstreret et angreb i 2015, der viste, at når de samme primtal blev brugt af mange servere som begyndelsen på nøgleudvekslingen, var den samlede sikkerhed for Diffie-Hellman lavere end forventet.

I det væsentlige kunne en angriber simpelthen forudkompute angrebet mod denne prime, hvilket gør det lettere at kompromittere sessioner for enhver server, der har brugt det primære nummer.

Dette skete, fordi millioner af servere brugte de samme primtal til nøgleudvekslinger. Forudbestemmelse af denne type angreb kræver stadig enten akademiske ressourcer eller nationalstatsniveau og er usandsynligt, at det påvirker langt de fleste mennesker.

Heldigvis for dem, der skal bekymre sig om nationstatsangreb, er der en anden måde at opnå DH-nøgleudvekslingen ved hjælp af elliptisk kurve kryptografi (ECDHE). Dette er ude af omfanget af denne artikel, men hvis du er interesseret i at lære mere om matematikken bag denne udveksling, kan du tjekke denne artikel.

For et mere detaljeret kig på DH’s svagheder, tjek denne whitepaper og dette websted.

RSA

RSA er opkaldt efter skaberne – Rivest, Shamir, Adleman – og det er en måde at generere offentlige og private nøgler.

Teknisk set er der to RSA -algoritmer (en, der bruges til digitale signaturer, og en, der bruges til asymmetrisk kryptering.) – Denne artikel dækker den asymmetriske krypteringsalgoritme.

Dette giver mulighed for nøgleudveksling – du tildeler først hver part til transaktionens offentlige/private nøgler, så genererer du en symmetrisk nøgle, og til sidst bruger du de offentlige/private nøglepar til sikkert at kommunikere den delte symmetriske nøgle sikkert.

Fordi asymmetrisk kryptering generelt er langsommere end symmetrisk kryptering, og det skaleres ikke også ved hjælp af asymmetrisk kryptering til sikkert at udveksle symmetriske taster er meget almindelig.

Så hvordan fungerer det?

1. Vælg 2 meget store primtal (mindst 512 bit eller 155 decimalcifre hver), x og y (disse tal skal være hemmelige og tilfældigt valgt)
2. Find produktet, dvs. z = x*y
3. Vælg et underligt offentligt heltal, E, mellem 3 og n – 1, og har ingen fælles faktorer (bortset fra 1) med (x -1) (y -1) (så det er relativt primært for x – 1 og y – 1 ).
4. Find den mindst almindelige multipel på x – 1 og y – 1, og kald det l.
5. Beregn den private eksponent, D, fra X, Y og E. de = 1 % l. D er det inverse af E % L (du ved, at der findes en omvendt, fordi E er relativt primær for Z – 1 og Y – 1). Dette system fungerer, fordi p = (p ^ e) ^ d % z.
6. Output (z, e) som den offentlige nøgle og (z, d) som den private nøgle.

Hvis Bob nu gerne vil sende en besked til Alice, genererer han chifferteksten (c) fra den almindelige tekst (p) ved hjælp af denne formel:

For at dekryptere denne meddelelse beregner Alice følgende:

Forholdet mellem D og E sikrer, at kryptering og dekrypteringsfunktioner er omvendt. Det betyder, at dekrypteringsfunktionen er i stand til med succes at gendanne den originale meddelelse, og at det er ret svært at gendanne den originale meddelelse uden den private nøgle (Z, D) (eller primefaktorer X og Y).

Dette betyder også, at du kan offentliggøre z og e uden at gå på kompromis med systemets sikkerhed, hvilket gør det let at kommunikere med andre, som du ikke allerede har en delt hemmelig nøgle.

Du kan også bruge operationerne omvendt for at få en digital underskrift af meddelelsen. Først bruger du dekrypteringsoperationen på The Plaintext. For eksempel s = signatur (p) = p ^ d % z.

Derefter kan modtageren verificere den digitale signatur ved at anvende krypteringsfunktionen og sammenligne resultatet med meddelelsen. For eksempel m = verificer (er) = s ^ e % z.

Ofte når dette er gjort, er The Plaintext en hash af meddelelsen, hvilket betyder, at du kan underskrive meddelelsen (uanset længde) med kun en eksponentiering.

Systemets sikkerhed er baseret på et par ting:

1. (Faktum) Det er relativt let at generere primtal, endda store primtal (som x og y).
2. (Fakta) Multiplikation er let. Det er meget let at finde z.
3. (Antagelse baseret på den aktuelle matematik) Faktorering er hård. Givet Z er det relativt svært at gendanne X og Y. Det kan gøres, men det tager et stykke tid, og det er dyrt.

Et estimat siger, at gendannelse af de vigtigste faktorer i et 1024-bit-nummer ville tage et år på en maskine, der koster 10 millioner dollars. Det ville eksponentielt øge den nødvendige arbejde (flere milliarder gange mere arbejde).

Efterhånden som teknologien fortsætter med at gå videre, vil disse omkostninger (og det krævede arbejde) falde, men på dette tidspunkt er denne type kryptering, korrekt implementeret, en usandsynlig kilde til kompromis.

Generelt er de eneste hackere med denne type penge og dedikation til et enkelt mål nationalstater. Plus, hvis der er en lettere måde at kompromittere et system (se nedenfor), er det sandsynligvis en bedre mulighed.

4. (Fakta) Modulær eksponentiering er let. Med andre ord er det relativt let at beregne c = p ^ e % z.

5. (Faktum) Modulær rodekstraktion – at vende processen ovenfor – er let, hvis du har de primære faktorer (hvis du har z, c, e og de primære faktorer x og y, er det let at finde p, så c = p ^ e % z).

6. (Antagelse baseret på den aktuelle computerkraft og matematik) Modulær rodekstraktion uden de vigtigste faktorer er meget hård (hvis du har z, c, e, men ikke x og y, er det relativt svært at finde p, så c = p ^ e % Z, især hvis A er tilstrækkelig stor).

Vil lære mere om matematik fra meget smartere mennesker? Tjek denne artikel.

Fantastisk, hvilket er bedre?

Det afhænger af din brugssag. Der er et par forskelle mellem de to algoritmer – først, Perfect Forward Secrecy (PFS), som vi talte om tidligere i sammenhæng med Diffie -Hellman. Mens du teknisk set er kunne Generer flygtig RSA-nøglepar, og giver perfekt fremadrettet hemmeligholdelse med RSA, beregningsomkostningerne er meget højere end for Diffie-Hellman-hvilket betyder, at Diffie-Hellman er et bedre valg for SSL/TLS-implementeringer, hvor du vil have perfekt fremadrettet hemmeligholdelse.

Mens der er nogle ydelsesforskelle mellem de to algoritmer (med hensyn til arbejde, der kræves fra serveren), er ydeevneforskellene generelt ikke store nok til at gøre en forskel, når man vælger den ene over den anden.

I stedet for generelt afhænger den primære overvejelse, når du bestemmer, hvad der er bedre, af hvilken der er mere understøttet til din brugssag (for eksempel når du implementerer SSL, du vil have Diffie Hellman på grund af perfekt fremadrettet hemmeligholdelse) eller hvilken er mere populær eller accepteret Som standarden i branchen.

For eksempel, mens Diffie -Hellman blev den amerikanske regering godkendt og støttet af et institutionelt organ, blev standarden ikke frigivet – mens RSA (standardiseret af en privat organisation) gav en gratis standard, hvilket betyder, at RSA blev meget populær blandt private organisationer.

Hvis du er interesseret i at læse mere, er der en god tråd her om forskellene.

Interesseret i at lære at hackere bruger kryptografiske angreb? Prøv dette sæt udfordringer fra kryptopaler.

Jo mere jeg lærer om kryptografi, jo mere synes jeg Alice og Bob sandsynligvis bare skal tale personligt.

– Paul Reinheimer (@Preinheimer) 13. marts 2017