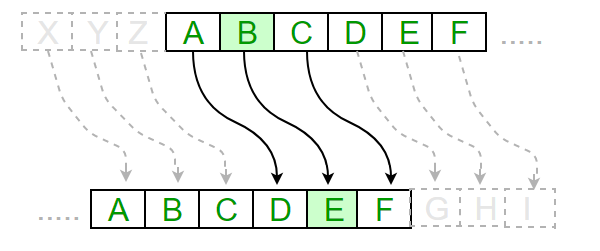
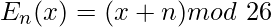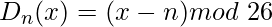Traditionelle chiffer

P → 16, O → 15, I → 9, N → 14 og T → 20.

Enkel substitutionsciffer

Den enkle substitutionsciffer er en chiffer, der har været i brug i mange hundreder af år (en fremragende historie er givet i Simon Singhs ‘The Code Book’). Det består dybest set af at erstatte enhver klagert karakter med en anden chiffertekst -karakter. Det adskiller.

Den enkle substitutionsciffer tilbyder meget lidt kommunikationssikkerhed, og det vil blive vist, at det let kan brydes selv med hånden, især når meddelelserne bliver længere (mere end flere hundrede chiffertekst -tegn).

Eksempel §

Her er et hurtigt eksempel på krypterings- og dekrypteringstrin, der er involveret i den enkle substitutionsciffer. Den tekst, vi krypterer, er ‘Forsvar den østlige væg af slottet’.

Nøgler til den enkle substitutionsciffer består normalt af 26 bogstaver (sammenlignet med Caeser Cipher’s enkelt nummer). Et eksempel på nøglen er:

Almindelig alfabet: abcdefghijklmnopqrstuvwxyz ciffer alfabet

Et eksempel på kryptering ved hjælp af ovenstående nøgle:

PLAINTEXT: Forsvar østvæggen på slottets chiffertekst: giuifg cei iprc tpnn du cei qprcni

Det er let at se, hvordan hver karakter i The Plaintext erstattes med det tilsvarende bogstav i cifferalfabetet. Dekryptering er lige så let ved at gå fra cifferalfabetet tilbage til det almindelige alfabet. Når man genererer nøgler, er det populært at bruge et nøgleord, e.g. ‘Zebra’ for at generere det, da det er meget lettere at huske et nøgleord sammenlignet med et tilfældigt virvar på 26 tegn. Ved hjælp af nøgleordet ‘Zebra’ ville nøglen blive:

Cipher Alphabet: Zebracdfghijklmnopqstuvwxy

Denne nøgle bruges derefter identisk til eksemplet ovenfor. Hvis dit nøgleord har gentagne tegn E.g. ‘Mammoth’, vær forsigtig med ikke at medtage de gentagne tegn i ciffer -alfabetet.

JavaScript -eksempel §

Andre implementeringer §

For at slå dine egne meddelelser i Python kan du bruge Pycipher -modulet. For at installere det skal du bruge PIP Installer Pycipher. For at indkalde beskeder med substitutionscifferen (eller en anden chiffer, se her for dokumentation):

>>> Fra Pycipher Import SimpleSubstitution >>> ss = SimpleSubstitution ('phqgiumeaylnofdxjkrcvstzwb') >>> ss.Encipher ('Forsvar den østlige væg af slottet') 'giuifgceiiprctpnnduceiqprcni' >>> ss.dechiffrer ('giuifgceiiprctpnnduceiqprcni') 'forsvarertheastwallofthecastle'

Kryptanalyse §

Se kryptanalyse af substitutionscifferen for en guide til, hvordan man automatisk bryder denne chiffer.

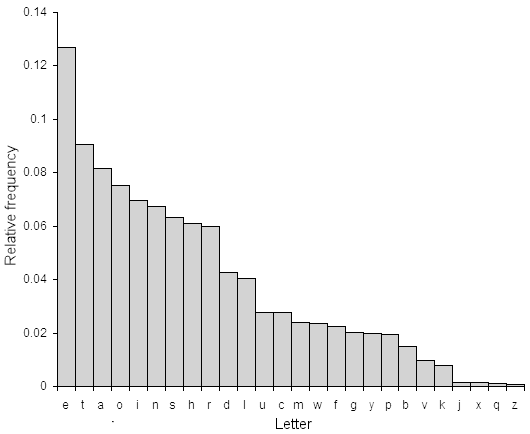
Den enkle substitutionsciffer er ret let at bryde. Selvom antallet af nøgler er omkring 2 88.4 (et rigtig stort antal), der er en masse redundans og andre statistiske egenskaber ved engelsk tekst, der gør det ganske let at bestemme en rimelig god nøgle. Det første trin er at beregne frekvensfordelingen af ​​bogstaverne i chiffereksten. Dette består af at tælle, hvor mange gange hvert bogstav vises. Naturlig engelsk tekst har en meget tydelig distribution, der kan bruges til at hjælpe revnekoder. Denne distribution er som følger:

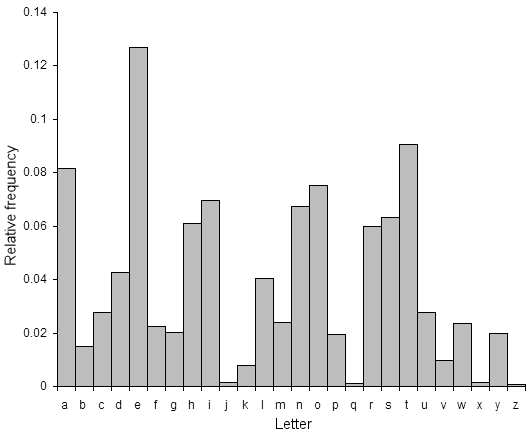
Dette betyder, at brevet ‘e’ er det mest almindelige og ser ud til næsten 13% af tiden, mens ‘z’ ser ud til langt mindre end 1 procent af tiden. Anvendelse af den enkle substitutionsciffer ændrer ikke disse bogstav frequncies, det kæmper dem blot lidt op (i eksemplet ovenfor, ‘e’ er indkapslet som ‘jeg’, hvilket betyder ‘jeg’ vil være den mest almindelige karakter i chifferet tekst). En kryptanalytiker skal finde den nøgle, der blev brugt til at kryptere meddelelsen, hvilket betyder at finde kortlægningen for hver karakter. For rimeligt store tekststykker (flere hundrede tegn) er det muligt bare at udskifte den mest almindelige chiffertekstkarakter med ‘E’, den næst mest almindelige chiffertekstkarakter med ‘T’ osv. For hver karakter (udskift i henhold til ordren på billedet til højre). Dette vil resultere i en meget god tilnærmelse af den originale sagsøger, men kun for tekststykker med statistiske egenskaber tæt på den for engelsk, som kun er garanteret for lange tekstområder.

Korte tekststykker har ofte brug for mere ekspertise for at knække. Hvis den originale tegnsætning findes i meddelelsen, e.g. ‘giuifg cei iprc tpnn du cei qprcni’, så er det muligt at bruge følgende regler til at gætte nogle af ordene, så ved hjælp af disse oplysninger er nogle af bogstaverne i chifferalfabetet kendt.

Ord med en bogstaver	a, i.
Hyppige ord med to bogstaver	af, til, i, er det, være, som, at, så, vi, han, ved eller, gør, hvis, hvis, mig, min, op, en, gå, nej, os, am
Hyppige ord med tre bogstaver	den og for, er, men ikke, du, alle, enhver, kan, have, hende, var, en, vores, ud, dag, få, har, ham, hans, hvordan, mand, ny, nu, nu, gammel, se, to, måde, hvem, dreng, gjorde, det, lad, sætte, siger, hun også bruger
Hyppige ord med fire bogstaver	Det med, har, dette, vil, din, fra, de ved, vil have, været, god, meget, nogle, tid

* Oplysningerne i ovenstående tabel blev lånt fra Simon Singhs websted, http: // www.Simonsingh.Net/The_Black_Chamber/tipsandtips.HTM

Normalt fjernes tegnsætning i chifferteksten, og chifferteksten sættes i blokke som ‘giuif gceii prctp nnduc eiqpr cnizz’, som forhindrer de foregående tricks i at arbejde. Der er dog mange andre egenskaber ved engelsk, der kan bruges. Nedenstående tabel viser nogle andre kendsgerninger, der kan bruges til at bestemme den korrekte nøgle. Kun de få mest almindelige eksempler er givet for hver regel.

For information om andre sprog, se brevfrekvenser for forskellige sprog.

Hyppigste enkelt bogstaver	E t a o i n s h r d l u
De fleste hyppige digrafer	th er på en re han i ed nd ha ved en eller nt ea ti til det st io le er ou ar as de rt ve
De fleste hyppige trigrafer	og tha ention tio for nde har nce edt tis ofte sth mænd
Mest almindelige dobbeltværelser	ss ee tt ff ll mm oo
Hyppigste indledende breve	T o a w b c d s f m r h i y e g l n p u j k
Hyppigste sidste bogstaver	E s t d n r y f l o g h a k m p u w

* Oplysningerne i ovenstående tabel blev lånt fra Simon Singhs websted, http: // www.Simonsingh.Net/The_Black_Chamber/tipsandtips.HTM

Der er flere tricks, der kan bruges ud over dem, der er anført her, måske en dag vil de blive inkluderet her. Brug i mellemtiden din foretrukne søgemaskine til at finde mere information.

Referencer §

• Wikipedia har en god beskrivelse af kryptering/dekrypteringsprocessen, historie og kryptanalyse af denne algoritme
• Simon Singhs ‘The Code Book’ er en fremragende introduktion til chiffer og koder og inkluderer et afsnit om substitutionscifre.
• Singh, Simon (2000). Kodebogen: Videnskaben om hemmeligholdelse fra det gamle Egypten til kvante kryptografi . ISBN 0-385-49532-3.

Simon Singhs websted har nogle gode substitutionscifferløsningsværktøjer:

• http: // www.Simonsingh.net/The_Black_chamber/frekvensanalyse.html
• http: // www.Simonsingh.Net/The_Black_Chamber/Frequencypuzzzle.HTM
• http: // www.Simonsingh.Net/The_Black_Chamber/tipsandtips.HTM

Traditionelle chiffer

I det andet kapitel drøftede vi de grundlæggende elementer i moderne kryptografi. Vi sidestilles med kryptografi med et værktøjssæt, hvor forskellige kryptografiske teknikker betragtes som de grundlæggende værktøjer. Et af disse værktøjer er den symmetriske nøglekryptering, hvor den nøgle, der bruges til kryptering og dekryptering, er den samme.

I dette kapitel diskuterer vi denne teknik yderligere og dens anvendelser om at udvikle forskellige kryptosystemer.

Tidligere kryptografiske systemer

Før du fortsætter videre, skal du kende nogle fakta om historiske kryptosystemer –

• Alle disse systemer er baseret på symmetrisk nøglekryptering ordning.
• Den eneste sikkerhedstjeneste, disse systemer leverer, er fortrolighed af information.
• I modsætning til moderne systemer, der er digitale og behandler data som binære tal, fungerede de tidligere systemer på alfabeter som grundlæggende element.

Disse tidligere kryptografiske systemer omtales også som chiffer. Generelt er en chiffer simpelthen bare et sæt trin (en algoritme) til udførelse af både en kryptering og den tilsvarende dekryptering.

Caesar -chiffer

Det er en mono-alfabetisk chiffer, hvor hvert bogstav i sagen er erstattet af et andet brev med at danne chifferteksten. Det er en enkleste form for substitutionscifferordning.

Dette kryptosystem kaldes generelt Skift chiffer. Konceptet er at erstatte hvert alfabet med et andet alfabet, der er ‘skiftet’ med et fast antal mellem 0 og 25.

For denne type ordning er både afsender og modtager enige om et ‘hemmeligt skiftnummer’ til at flytte alfabetet. Dette nummer, der er mellem 0 og 25, bliver nøglen til kryptering.

Navnet ‘Caesar Cipher’ bruges lejlighedsvis til at beskrive skiftcifferen, når ‘skiftet af tre’ bruges.

Proces med skiftciffer

• For at kryptere et ClaintExt -brev, placerer afsender.
• Plaintext -brevet er derefter krypteret til chiffertekst -brevet på den glidende lineal nedenunder. Resultatet af denne proces er afbildet i følgende illustration for et aftalt skift af tre positioner. I dette tilfælde krypteres den claintext ‘tutorial’ til chifferteksten ‘WXWROLDO’. Her er chiffertekst -alfabetet for et skift på 3 –

• Efter at have modtaget chifferteksten, placerer modtageren, der også kender det hemmelige skift, sin glidende lineal under chiffertekst -alfabetet og glider det til højre ved det aftalte skiftnummer, 3 i dette tilfælde.
• Derefter erstatter han Ciffertext -brevet med The Plaintext -brevet om den glidende lineal nedenunder. Derfor er chifferteksten ‘Wxwruldo’ dekrypteret til ‘tutorial’. For at dekryptere en meddelelse, der er kodet med et skift på 3, skal du generere The PlaintExt-alfabetet ved hjælp af et skift af ‘-3’ som vist nedenfor-

Sikkerhedsværdi

Caesar Cipher er ikke en sikker kryptosystem, fordi der kun er 26 mulige nøgler at prøve. En angriber kan udføre en udtømmende nøglesøgning med tilgængelige begrænsede computerressourcer.

Enkel substitutionsciffer

Det er en forbedring af Caesar -chifferet. I stedet for at skifte alfabeter med et eller andet antal, bruger denne ordning en vis permutation af bogstaverne i alfabetet.

For eksempel a.B ….Y.Z og z.Y …… b.A er to åbenlyse permutation af alle bogstaver i alfabetet. Permutation er intet andet end et virvlet sæt alfabeter.

Med 26 bogstaver i alfabetet er de mulige permutationer 26! (Factorial of 26), som er lig med 4×10 26 . Afsenderen og modtageren kan vælge en af ​​disse mulige permutation som et chiffertekst -alfabet. Denne permutation er den hemmelige nøgle for ordningen.

Proces med enkel substitutionsciffer

• Skriv alfabetterne A, B, C. Z I den naturlige orden.
• Afsenderen og modtageren beslutter en tilfældigt valgt permutation af bogstaverne i alfabetet.
• Under de naturlige orden alfabeter, skriv den valgte permutation af bogstaverne i alfabetet. For kryptering erstatter afsenderen hver af sigtekst -bogstaver ved at erstatte permutationsbrevet, der er direkte under det i tabellen. Denne proces er vist på følgende illustration. I dette eksempel er den valgte permutation K, D, G, . O. Raintext ‘Point’ er krypteret til ‘MJBXZ’.

Her er et virvlet chiffertekst -alfabet, hvor rækkefølgen af ​​chiffertekstbrevene er en nøgle.

• Ved modtagelse af chifferteksten erstatter modtageren, der også kender den tilfældigt valgte permutation. Cifferteksten ‘MJBXZ’ er dekrypteret til ‘Point’.

Sikkerhedsværdi

Enkel substitutionsciffer er en betydelig forbedring i forhold til Caesar -chifferen. Det mulige antal nøgler er stort (26!) og endda de moderne computersystemer er endnu ikke kraftige nok til komfortabelt at starte et brute force -angreb til at bryde systemet. Imidlertid har den enkle substitutionsciffer et simpelt design, og det er tilbøjeligt til at designe mangler, siger at vælge åbenlyst permutation, dette kryptosystem kan let brydes.

Monoalfabetisk og polyalphabetisk chiffer

Monoalfabetisk chiffer er en substitutionsciffer, hvor chiffer alfabetet for et givet nøgle for en given nøgle er fastgjort i hele krypteringsprocessen. For eksempel, hvis ‘A’ er krypteret som ‘D’, for et vilkårligt antal forekomster i denne PLAINTEXT, vil ‘A’ altid blive krypteret til ‘D’.

Alle substitutionsciffer, vi har drøftet tidligere i dette kapitel, er monoalfabetiske; Disse chiffer er meget modtagelige for kryptanalyse.

Polyalphabetic Cipher er en substitutionsciffer, hvor chiffer alfabetet til det almindelige alfabet kan være forskellige på forskellige steder under krypteringsprocessen. De næste to eksempler, Playfair og Vigenere Cipher er polyalfabetiske chiffer.

Playfair Cipher

I denne ordning er par breve krypteret i stedet for enkelt bogstaver som i tilfældet med simpel substitutionsciffer.

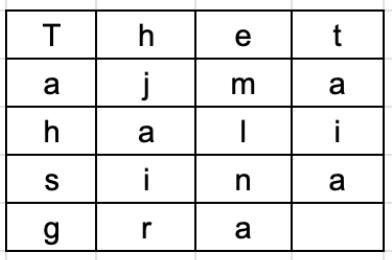
I Playfair Cipher oprettes oprindeligt en nøglebord. Nøglebordet er et 5 × 5 gitter af alfabeter, der fungerer som nøglen til at kryptere The PlaintExt. Hver af de 25 alfabeter skal være unikke, og et bogstav i alfabetet (normalt j) udelades fra tabellen, da vi kun har brug for 25 alfabeter i stedet for 26. Hvis The Plaintext indeholder J, erstattes den med i.

Afsenderen og modtagerdeicidet på en bestemt nøgle, siger ‘tutorials’. I en nøglebord er de første tegn (går til venstre til højre) i tabellen sætningen, eksklusive duplikatbrevene. Resten af ​​tabellen vil blive fyldt med de resterende bogstaver i alfabetet i naturlig rækkefølge. Nøglebordet fungerer at være –

Proces med playfair ciffer

• For det første er en PlaintExt -meddelelse opdelt i par to bogstaver (digraphs). Hvis der er et underligt antal bogstaver, tilføjes en z til det sidste brev. Lad os sige, at vi ønsker at kryptere meddelelsen “Skjul penge”. Det vil blive skrevet som – hej de mo ne yz
• Reglerne for kryptering er –
  • Hvis begge bogstaver er i den samme kolonne, skal du tage brevet under hver enkelt (gå tilbage til toppen, hvis det er i bunden)

  T	U	O	R	jeg	‘H’ og ‘jeg’ er i samme kolonne, og tag derfor brev under dem for at erstatte. Hej → QC
  EN	L	S	B	C
  D	E	F	G	H
  K	M	N	S	Q
  V	W	x	Y	Z

  T	U	O	R	jeg	‘D’ og ‘E’ er i samme række, og tag derfor brev til højre for dem at erstatte. De → Ef
  EN	L	S	B	C
  D	E	F	G	H
  K	M	N	S	Q
  V	W	x	Y	Z

  

• Hvis ingen af ​​de foregående to regler er sande, skal du danne et rektangel med de to bogstaver og tage bogstaverne på det vandrette modsatte hjørne af rektanglet.

Ved hjælp af disse regler ville resultatet af kryptering af ‘skjule penge’ med nøglen til ‘tutorials’ være –

At dekryptere Playfair -chifferen er så enkel som at gøre den samme proces i omvendt. Modtageren har den samme nøgle og kan oprette den samme nøglebord og derefter dekryptere alle meddelelser, der er lavet ved hjælp af den nøgle.

Sikkerhedsværdi

Det er også en substitutionsciffer og er vanskelig at bryde sammenlignet med den enkle substitutionsciffer. Som i tilfælde af substitutionsciffer er kryptanalyse også mulig på Playfair -chifferen, men det ville være mod 625 mulige par bogstaver (25×25 alfabeter) i stedet for 26 forskellige mulige alfabeter.

Playfair-chifferen blev hovedsageligt brugt til at beskytte vigtige, men alligevel ikke-kritiske hemmeligheder, da det er hurtigt at bruge og kræver intet specielt udstyr.

Vigenere Ciffer

Denne skema med chiffer bruger en tekststreng (f.eks.

Lad os for eksempel antage, at nøglen er ‘punkt’. Hvert alfabet af nøglen konverteres til dets respektive numeriske værdi: I dette tilfælde,

P → 16, O → 15, I → 9, N → 14 og T → 20.

Således er nøglen: 16 15 9 14 20.

Proces med Vigenere -chiffer

• Afsenderen og modtageren beslutter en nøgle. Sig ‘punkt’ er nøglen. Numerisk repræsentation af denne nøgle er ’16 15 9 14 20 ‘.
• Afsenderen ønsker at kryptere beskeden, siger ‘angreb fra South East’. Han vil arrangere enheden og numerisk nøgle som følger –

• Han skifter nu hvert PLAINTEXT -alfabet efter antallet, der er skrevet nedenfor for at oprette chiffertekst som vist nedenfor –

• Her er hver PLAINTEXT -karakter blevet skiftet med et andet beløb – og det beløb bestemmes af nøglen. Nøglen skal være mindre end eller lig med størrelsen på meddelelsen.
• Til dekryptering bruger modtageren den samme nøgle, og skift modtaget chiffertekst i omvendt rækkefølge for at få The PlaintExt.

Sikkerhedsværdi

Vigenere Cipher blev designet ved at finpusse standard Caesar -chiffer for at reducere effektiviteten af ​​kryptanalyse på chifferteksten og gøre et kryptosystem mere robust. Det er markant mere sikker end en almindelig Cæsar -chiffer.

I historien blev den regelmæssigt brugt til at beskytte følsom politisk og militær information. Det blev omtalt som Ubrydelig chiffer På grund af vanskeligheden udgjorde det kryptanalysen.

Varianter af Vigenere Cipher

Der er to specielle tilfælde af Vigenere -chiffer –

• Nøgleordets længde er den samme som en sagsøger besked. Denne sag kaldes Vernam Cipher. Det er mere sikkert end typisk Vigenere -chiffer.
• Vigenere Ciffer bliver et kryptosystem med perfekt hemmeligholdelse, der kaldes Engangs pude.

Engangs pude

Omstændighederne er –

• Længden af ​​nøgleordet er den samme som længden af ​​den sagsøger.
• Nøgleordet er en tilfældigt genereret række alfabeter.
• Nøgleordet bruges kun én gang.

Sikkerhedsværdi

Lad os sammenligne skift-chiffer med engangspude.

Skift chiffer – let at bryde

I tilfælde af skift -chiffer kunne hele meddelelsen have haft et skift mellem 1 og 25. Dette er en meget lille størrelse og meget let at brute kraft. Men med hver karakter, der nu har sit eget individuelle skift mellem 1 og 26, vokser de mulige taster eksponentielt for meddelelsen.

Engangspude-umulig at bryde

Lad os sige, vi krypterer navnet “punkt” med en engangspude. Det er en 5 -bogstekst. For at bryde chifferteksten med brute force skal du prøve alle muligheder for nøgler og udføre beregning for (26 x 26 x 26 x 26 x 26) = 26 5 = 11881376 gange. Det er til en meddelelse med 5 alfabeter. For en længere meddelelse vokser beregningen således eksponentielt med hvert ekstra alfabet. Dette gør det beregningsmæssigt umuligt at bryde chifferteksten ved brute force.

Transposition Ciffer

Det er en anden type chiffer, hvor rækkefølgen af ​​alfabetterne i sagsøgeren omarrangeres for at skabe chifferteksten. De faktiske rentext -alfabeter erstattes ikke.

Et eksempel er en ‘simpel kolonne transposition’ -ciffer, hvor The Plaintext er skrevet vandret med en bestemt alfabetbredde. Så læses chifferteksten lodret som vist.

F.eks. Vi arrangerer denne tekst vandret i tabel med antallet af kolonne, der er lig med nøgleværdien. Den resulterende tekst er vist nedenfor.

Cifferteksten opnås ved at læse søjle lodret nedad fra første til sidste kolonne. Cifferteksten er ‘GnuneaoseenvltiltedaseHetivc’.

For at dekryptere forbereder modtageren lignende tabel. Antallet af kolonner er lig med nøglenummeret. Antallet af rækker opnås ved at dele antal samlede chiffertekst -alfabeter efter nøgleværdi og afrunding af kvotienten til næste heltalværdi.

Modtageren skriver derefter den modtagne chiffertekst lodret ned og fra venstre mod højre kolonne. For at få teksten læser han vandret fra venstre til højre og fra top til bund række.

Kickstart din karriere

Bliv certificeret ved at gennemføre kurset

Caesar -chiffer i kryptografi

(Krypteringsfase med skift n)

(Dekrypteringsfase med skift n)

Eksempler:

Tekst : Abcdefghijklmnopqrstuvwxyz Flytte: 23 Chiffer: Xyzabcdefghijklmnopqrstuvw Tekst : Attackatonce Flytte: 4 Chiffer: Exxegoexsrgi

Fordele:

• Let at implementere og bruge således, hvilket gør det egnet til begyndere at lære om kryptering.
• Kan implementeres fysisk, f.eks. Med et sæt roterende diske eller et sæt kort, kendt som en Scytale, som kan være nyttig i visse situationer.
• Kræver kun et lille sæt oplysninger før delte.
• Kan let ændres for at skabe en mere sikker variant, f.eks. Ved at bruge en flere skiftværdier eller nøgleord.

Ulemper:

• Det er ikke sikkert mod moderne dekrypteringsmetoder.
• Sårbare over for angreb på kendte-plaintekst, hvor en angriber har adgang til både de krypterede og ikke-krypterede versioner af de samme meddelelser.
• Det lille antal mulige nøgler betyder, at en angriber let kan prøve alle mulige nøgler, indtil den rigtige findes, hvilket gør det sårbart over for et brute force -angreb.
• Det er ikke egnet til lang tekstkryptering, da det ville være let at knække.
• Det er ikke egnet til sikker kommunikation, da det let er brudt.
• Giver ikke fortrolighed, integritet og ægthed i en meddelelse.

Funktioner af Caesar -chiffer:

1. Substitutionsciffer: Caesar -chifferen er en type substitutionsciffer, hvor hvert bogstav i The PlaintExt erstattes af et bogstav, som et fast antal positioner ned ad alfabetet.
2. Fast nøgle: Caesar -chifferet bruger en fast nøgle, som er antallet af positioner, hvormed bogstaverne forskydes. Denne nøgle er kendt for både afsenderen og modtageren.
3. Symmetrisk kryptering: Caesar -chifferen er en symmetrisk krypteringsteknik, hvilket betyder, at den samme nøgle bruges til både kryptering og dekryptering.
4. Begrænset tasterområde: Caesar -chifferet har et meget begrænset tastelrum på kun 26 mulige nøgler, da der kun er 26 bogstaver i det engelske alfabet.
5. Vårlig over for brute force -angreb: Caesar -chifferen er sårbar over for brute force -angreb, da der kun er 26 mulige nøgler til at prøve.
6. Let at implementere: Caesar -chiffer er meget let at implementere og kræver kun enkle aritmetiske operationer, hvilket gør det til et populært valg til enkle krypteringsopgaver.

Regler for Caesar -chiffer:

1. Vælg et nummer mellem 1 og 25. Dette vil være din “skift” -værdi.
2. Skriv alfabetets bogstaver ned i orden, fra a til z.
3. Skift hvert bogstav i alfabetet med “skift” -værdien. For eksempel, hvis skiftværdien er 3, ville a blive d, b ville blive e, c ville blive f, og så videre.
4. Krypter din besked ved at erstatte hvert brev med det tilsvarende skiftede brev. For eksempel, hvis skiftværdien er 3, ville ordet “hej” blive “khoor”.
5. For at dekryptere meddelelsen skal du blot vende processen ved at skifte hvert brev tilbage med det samme beløb. For eksempel, hvis skiftværdien er 3, ville den krypterede meddelelse “Khoor” blive “hej”.

Algoritme til Caesar -chiffer:
Input:

1. Vælg en skiftværdi mellem 1 og 25.
2. Skriv alfabetet ned i rækkefølge fra a til z.
3. Opret et nyt alfabet ved at skifte hvert bogstav i det originale alfabet ved skiftværdien. For eksempel, hvis skiftværdien er 3, ville det nye alfabet være:
4. A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
   D E F G H I J K L M N O P Q R S T U V W X Y Z A B C
5. Udskift hvert brev i meddelelsen med det tilsvarende bogstav fra det nye alfabet. For eksempel, hvis skiftværdien er 3, ville ordet “hej” blive “khoor”.
6. For at dekryptere meddelelsen skal du skifte hvert brev tilbage med det samme beløb. For eksempel, hvis skiftværdien er 3, ville den krypterede meddelelse “Khoor” blive “hej”.

Procedure:

• Krydse den givne tekst en karakter ad gangen .
• For hver karakter skal du transformere den givne karakter i henhold til reglen, afhængigt af om vi krypterer eller dekrypterer teksten.
• Returner den nye streng, der er genereret.

Et program, der modtager en tekst (streng) og skiftværdi (heltal) og returnerer den krypterede tekst.